when the small intestine is stimulated by the entrance
of fats.
THE URINARY SYSTEM
LEARNING OBJECTIVE: Recall the parts
of the urinary system and their function(s).
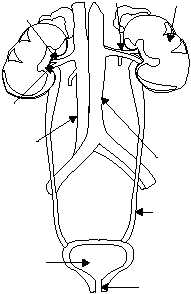
The urinary system is the primary filtering system
of the body (fig. 1-55). This system is composed of two
main organs, the kidneys and urinary bladder. The
kidneys produce urine, which is drained from the
kidneys by two tubes called ureters. Urine flows down
both ureters to the bladder. The urinary bladder is a
large reservoir where the urine is temporarily stored
before excretion from the body. A tube called the
urethra carries the urine from the bladder to the
outside of the body. All these parts, except the length of
the urethra, are the same in both sexes.
KIDNEYS
The importance of the kidney can be realized only
when its structure and functions are understood. The
bladder, ureters, and urethra store and pass the
products of the kidneys.
The kidneys are two large, bean-shaped organs
designed to filter waste materials from the blood (figs.
1-55 and 1-56). They also assist in controlling the rate
of red blood cell formation, and in the regulation of
blood pressure, the absorption of calcium ions, and the
volume, composition, and pH of body fluids. The
kidneys are located in the upper posterior part of the
abdominal cavity, one on each side of the spinal
column. The upper end of each kidney reaches above
the level of the 12th rib. The suprarenal (adrenal) gland
sits like a cap on top of each kidney. The kidneys are
protected by a considerable amount of fat and
supported by connective tissue and the peritoneum.
Attached to the hollow side of each kidney is the
dilated upper end of the ureter, forming the renal
pelvis.
Structure
The lateral surface of the kidneys is convex in
shape, and the medial side is deeply concave. The
medial side of each kidney possesses a depression that
leads to a hollow chamber called the renal sinus (fig.
1-55). The entrance of the renal sinus is referred to as
the hilum (fig. 1-55). Blood vessels, nerves, lymphatic
vessels, and the ureters pass through the hilum.
T h e s u p e r i o r e n d o f t h e u r e t e r f o r m s a
funnel-shaped sac called the renal pelvis (fig. 1-56).
The renal pelvis is divided into two or three tubes,
called major calyces. The major calyces (sing. calyx)
are further subdivided into minor calyces.
There are groups of elevated projections in the
walls of the renal pelvis. These projections are called
renal papillae. The renal papillae connect to the minor
calyces, through tiny openings in the minor calyces.
The principal portion of the kidney is divided into
two distinct regions: an inner medulla and outer cortex
(fig. 1-56). The renal medulla is composed of
pyramid-shaped masses of tubes and tubules called
renal pyramids. Renal pyramids drain the urine to
the renal pelvis. The renal cortex forms a shell over
the renal medulla. Renal cortex tissue dips down, like
fingers, between the renal pyramids, and forms what
are called renal columns. The cortex possesses very
small tubes associated with nephrons. Nephrons are
the functional units of the kidneys.
RENAL BLOOD VESSELS.—The renal artery
supplies blood to the kidneys (fig. 1-56). The renal
artery enters the kidneys through the hilum, and sends
off branches to the renal pyramids. These arterial
branches are called interlobar arteries. At the border
between the medulla and cortex, the interlobar arteries
branch to form the arciform arteries. The arciform
arteries branch also and form the interlobular
arteries.
1-53
HM3F0155
RENAL
ARTERY
KIDNEY
RENAL
SINUS
AORTA
URETER
URETHRA
URINARY
BLADDER
INFERIOR
VENA
CAVA
HILUM
RENAL
VEIN
Figure 1-55.—The urinary system.