cortex to form a collecting duct. The collecting duct
begins to merge within the renal medulla. The
collecting ducts become increasingly larger as they are
joined by other collecting ducts. The resulting tube is
called the papillary duct. The papillary duct empties
into the minor calyx through an opening in the renal
papilla.
Function
The kidneys are effective blood purifiers and fluid
balance regulators. In addition to maintaining a normal
pH of the blood (acid-base balance), the kidneys keep
the blood slightly alkaline by removing excess
substances from the blood. The end product of these
functions is the formation of urine, which is excreted
from the body.
Urine is formed through a series of processes in the
nephron. These processes are filtration, reabsorption,
and secretion.
FILTRATION.—Urine formation begins when
water and various dissolved substances are filtered out
of blood plasma from a glomerular capillary into the
glomerular capsule. The filtered substance (glomerular
filtrate) leaves the glomerular capsule and enters the
renal tubule.
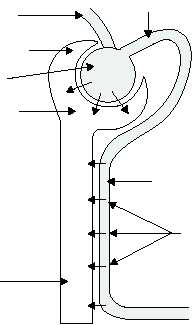
REABSORPTION.—As glomerular filtrate
passes through the renal tubule, some of the filtrate is
reabsorbed into the blood of the peritubular capillary
(fig. 1-57). The filtrate entering the peritubular
capillary will repeat the filtration cycle. This process
of reabsorption changes the composition of urine. For
instance, the filtrate entering the renal tubule is high in
sugar content, but because of the reabsorption process,
urine secreted from the body does not contain sugar.
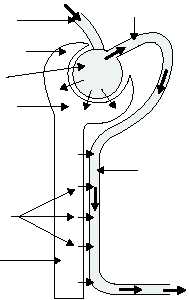
SECRETION.—Secretion is the process by
which the peritubular capillary transports certain
substances directly into the fluid of the renal tubule
(fig. 1-58). These substances are transported by similar
mechanisms as used in the reabsorption process, but
done in reverse. For example, certain organic
compounds, such as penicillin and histamine, are
secreted directly from the proximal convoluted tubule
to the renal tubule. Also, large quantities of hydrogen
ions are secreted in this same manner. The secretion of
hydrogen ions plays an important role in regulating pH
of body fluids.
The glomerulus filters gallons of blood each day. It
is estimated that 2,500 gallons of blood pass through
the kidneys in 24 hours, and about 80 gallons of
glomerular filtrate. All the water from this filtrate is
reabsorbed in the renal tubules except that containing
the concentrated waste products.
1-55
HM3F0158
EFFERENT
ARTERIOLE
AFFERENT
ARTERIOLE
GLOMERULAR
CAPSULE
GLOMERULUS
GLOMERULAR
FILTRATE
RENAL
TUBULE
PERITUBULAR
CAPILLARY
SECRETION
Figure 1-58.—The secretion process.
HM3F0157
EFFERENT
ARTERIOLE
BLOOD
FLOW
AFFERENT
ARTERIOLE
GLOMERULAR
CAPSULE
GLOMERULUS
GLOMERULAR
FILTRATE
REABSORPTION
RENAL
TUBULE
PERITUBULAR
CAPILLARY
BLOOD
FLOW
Figure 1-57.—The reabsorption process.