as of Rules for solving ratio solution problems are follows:
W/W solution: Divide the total weight (grams) solution desired by the larger number of the ratio, and the quotient will be the number of grams of the solute to be used.
Example: How many grams of KMNO4 are needed to make 500 g of a 1:2000 solution?
500 ÷ 2000 = 0.25 g of drug needed.
500 - 0.25 = 499.75 g of solvent needed.
W/V solution: Divide the total volume in ml of solution desired by the larger number of the ratio, and the quotient will be the number of grams of the solute needed.
Example: How many grams of bichloride of mercury are needed to prepare 500 ml of a 1:1000 solution?
5OO ÷ 1000 = 0.5 g of drug needed.
Take 0.5 g of the drug and add sufficient (q.s. with) solvent to make 500 ml; this gives you 1:1000 strength.
V/V Solution: Divide the total volume in ml of the solution desired by the larger number of the ratio, and the quotient will be the number of ml of the drug to be used.
Example: How many milliliters of HCl would be used to prepare a 1:250 solution with the total volume to be 500 ml?
500 ÷ 250 = 2 ml of HCl needed
Percentage solutions from stock and/or ratio solutions:
Example: From a 1:10 solution of silver nitrate in water, prepare 60 ml of a 1.5% solution of the same ingredients.
A 1:10 (W/V) solution contains 1 g of solute and enough solvent (q.s.) to total a 10 ml solution (finished product). Therefore, 1 ml of the solution would contain 0.1 g of the solute. Since it is required that 0.9 g of the solute be used to prepare 60 ml of the required strength, use 9 ml
of the stock solution and enough solvent (water) to make the total volume measure 60 ml.
SPECIFIC GRAVITY
Specific gravity is the ratio of the weight of a given substance to the weight of an equal volume of a substance chosen as a standard. It is a means of determining the strength, purity, or volume of a substance. Water is the chosen substance as the standard for solids and liquids.
It is known that water has a unit weight of 1 g per ml of space occupied. Basic formulas predicated on this information are as follows:
ml x S/G = weight
weight/(S/G) = ml
weight/ml = S/G
Sample problems:
1. What is the weight in grams of 300 ml of alcohol with a specific gravity of 0.8?
ml x S/G = wt ..... 300 x 0.8 = 240g
2. 900 g of glycerine with a S/G of 1.25 would measure how many milliliters?
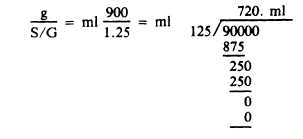
3. If 50 ml of a liquid has a weight of 50.5 g, what is the specific gravity?
wt/ml = S/G ... 50.5/50 = 1.01 ... S/G = 1.01
COMPOUNDING
By definition, compounding implies the various processes and procedures required to manufacture a pharmaceutical preparation for dispensing to the patient. The art of compounding is a profession in itself, and a great deal more
