Percentage in that respect means parts of active ingredient per 100 parts of total preparation. The three basic rules to remember in solving percentage problems are:
1. To find the amount of the active ingredient when the percentage strength and the total quantity ARE known, multiply the total weight or volume by the percent (expressed as a decimal fraction).
Example: Substance X contains 38% fat. How many grams of fat are required to prepare 120 g of substance X?
Solution: 38% is expressed as a decimal fraction 0.38 and multiplied by the amount of the finished product required.
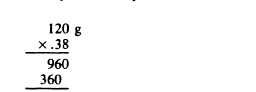
45.60 g—the weight of fat needed.
2. To find the total quantity of a mixture when the percentage strength and the amount of the active ingredient are known, divide the weight or volume of the active ingredient by the percent (expressed as a decimal fraction).
Example: If a mixture contains 20% of substance Y, how many grams of the 20% mixture would contain 8 g of Y?
Solution: 20% is expressed as a decimal fraction 0.20. Divide the weight (8 g) by the percent, thus;
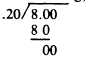
40.0 g, the weight of 20% mixture that would contain 8 g of substance Y.
3. To find the percentage strength when the amount of the active ingredient and the total quantity of the mixture are known, divide the weight or volume of the active ingredient by the total weight or volume of the mixture. Multiply the resulting answer by 100 to convert the decimal fraction to percent.
Example: Find the percentage strength of Z if 300 g of a mixture contains 90 g of substance Z.
Solution:
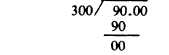
0.3 g, is the percent of Z expressed as a decimal fraction.
0.3 x 100 (%) = 30% of Z in the mixture.
Alternate Method for Solving Percentage Problems
The alternate method for solving percentage problems incorporates the three rules discussed above into one equation. This method is often preferred since it eliminates errors that may result from misinterpreting the facts given in the problem.
1. Percent strength = Amount of active ingredient x 100(%) Total amount of preparation
Examples:
a. Calculate the percent of A in a solution if 120 g of solution contains 6 g of A.
Solution: Substitute the known facts in the equation and use X for percent (the unknown factor).
X = 6/120 x 100(%) = 5(%)
Therefore X = 5, which is the percent strength of the solution.
b. Calculate the amount of active ingredient m 300 g of a 5070 mixture of active ingredient B.
Solution: Convert 5% to a decimal fraction 0.05. Substitute the known facts in the equations and use X for the amount of active ingredient (unknown).
0.05 = X/300 X = 15g
2. A variation of equation 1 uses “parts per hundred” instead of percent with X used as the unknown.
Amount of active ingredient / Amount of total preparation = Parts of active ingredient / 100 parts (total mixture)
